1 引 言
20 世纪 80年代到 21世纪初,我国港口集装箱吞吐量每年以两位数的百分比递增。我国港口集装箱吞吐量从 1986 年的62.7万TEU增加到了 2001 年底的2 500 万TEU,16年期间增加到近 40倍。我国的对外贸易额从 1986年的 738.5亿美元增加了 2001底的 5 018亿美元,16年共增加了近 6倍。后世贸时代,航运界人士将格外关注我国港口集装箱吞吐量的变化,本文将以数学模型对此问题进行研究。
2 港口集装箱吞吐量与对外贸易额相关性回归模型
2.1 模型的假定
为寻找我国主要港口集装箱吞吐量与对外贸易额的相关性,我们设定回归模型为 2.2 估计的回归方程
我们按照 将数据输入到 Excel中计算,分别得到:
为此,我们得到了对外贸易额在过去16年的平均值(X)为 2 360.4,港口集装箱吞吐量在过去 16 年的平均值(Y)为739.48(计算过程省略)。根据上述值,我们分别把数据代进公式(1)中,我们得到 b1=0.543,b0=-542.22,为此,我们得到了 3 验 证
的对外贸易额与港口集装箱吞吐量的回归方程,只是对上述线性方程的一个近似的表述,它并不能完全代表贸易额与集装箱吞吐量之间的线性关系,因此,应对上述方程用统计学原理进行判定系数的验证,以证明对外贸易额与主要港口集装箱吞吐量之间的线性关系,即我们平常所说的拟合优度。用 如果港口集装箱吞吐量的每一个值(Yi)准确无误地落在Y的估计回归方程的直线上时,那么港口集装箱的估计回归方程将出现一个 100%的拟合。如果这样,对于每一个港口吞吐量观测值都将等于0,进而导致SSE(误差平方和)等于0,就此得出结论:SSE 的值在趋于 0时,则港口集装箱吞吐量的估计方程值拟合度比较好,反之则差,即SSE的值越大,港口集装箱吞吐量的估计方程值拟合优度越差。经计算经计算r2=SSR/SST=(8200 200/8 664 600)×100%=94.64%。毫无疑问,r2(判定系数)是总平方和中能被估计的港口集装箱吞吐量的回归方程解释的百分比。在用 的回归方程去预测主要港口集装箱吞吐量与对外贸易额时,我们能判定,总平方和的94.64%能被估计的回归方程所解释。对于近似于一个95%的解释港口集装箱吞吐量与对外贸易额的线性关系,我们为能得到这样一个令人满意的拟合优度而高兴。
2) 尽管对表述拟合优度的判定系数进行了检验,但还没有对 Y的港口集装箱吞吐量回归方程的相关系数进行检验。相关系数值是介于-1与+1之间的数值。如果相关系数的值 bi≤0或bi =1,则表明港口集装箱吞吐量(Y)与对外贸易额(X)之间是 100%正相关,即所有的数据点都落在一条斜线率为正的直线上;如果相关系数的值bi <0或bi =-1,则表明港口集装箱吞吐量(Y)与对外贸易额(X)之间是 100%负相关,即所有的数据点都落在一条斜线率为负的直线上。
港口集装箱吞吐量(Y)与对外贸易额(X)之间的相关系数 rxy=97.28%,所以,有理由判定X和 Y之间存在着一个强势正向线性关系。
3) 在利用最小二乘法求导出的估计回归方程和计算判定系数及相关系数时,我们没有做概率分析,也没有对对外贸易额(X)和港口集装箱吞吐量(Y)之间关系的显著性做检验。港口集装箱吞吐量(Y)的平均值或期望值是对外贸易额(X)的一个线性函数: 那么港口集装箱吞吐量(Y)的平均值或期望值不依赖于对外贸易额(X)的值。因此,结论是:港口集装箱吞吐量与对外贸易额之间不存在线性关系。为此,检验变量间是否存在一个显著的回归关系就须引入判定 (1) 对δ2的检验。 MSE 是δ2的一个无偏估计量,记着S2均方误差(δ2的估计量)S2=SSE/(n-2)= 464 399/(16-2)=33 171。
( 2 ) 估计量的标准误差。S = (S S E /(n -2))(1/2) = (464 399/(16-2))(1/2)=182。由此,可以得到这样的结论:在港口集装箱吞吐量与对外贸易额的回归方程中, (3) t 检验。t 检验是我们能否拒绝 H0: β1= 0 , Hα : β1≠ 0 。如果 H0被否定,那么β10,于是,在港口集装箱吞吐量与对外贸易额之间存在着一个统计学上显著的关系,否则就没有理由证明港口集装箱吞吐量和对外贸易之间存在着一个显著的关系。根据拒绝法则,如果 t<-ta/2或 t> ta/2 ta/2,则拒绝H0,ta/2是 X 水平的自由度为 n-2 的分布的双侧分位数。检验统计量 t=b1/S,bi=0.543/0.035=15.7。取α=0.01,自由度为n-2=16-2=14 的 t 分布双侧分位数是 t0.005=2.977,很显然15.7>2.97,因此,拒绝 H0,有足够的理由证明在显著性水平X=0.01下,β1显著,β1=0,换句话说,港口集装箱吞吐量与对外贸易额之间存在着一个显著的关系。
4港口集装箱回归模型的预测与检验
港口集装箱回归模型是对外贸易额(X)的变量与港口集装箱吞吐量(Y)之间关系的假设。利用该模型方程,可以获得对外贸易额(X)在某一个点与之对应的港口集装箱的对应值,如对外贸易额在 4743亿美元(2000年进出口总额)时,我文章有条评论 采用最小二乘法
采用最小二乘法 的估计值
的估计值 将得到估计的回归:
将得到估计的回归: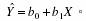
 的准则,分别按下列公式导出港口集装箱应变量的观测值
的准则,分别按下列公式导出港口集装箱应变量的观测值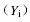 和估计值
和估计值 :
:


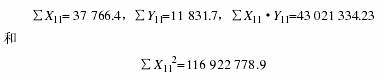
 的我国主要港口集装箱吞吐量与对外贸易相关性回归的估计方程。在这里港口集装箱吞吐量的估计回归方程的斜率(b1=0.543)是正的,说明随着我国对外贸易额的增长,港口集装箱吞吐量也随之增加。确切地说,如果我国对外贸易额每增加 1 亿美元,港口集装箱吞吐量将增加 5 430TEU,我们还可以说,对外贸易额每增加 1 个百分点,主要港口集装箱吞吐量将增加 0.543 个百分点,反之亦然。应用最小二乘法得到的估计的回归方程似乎可以满意地描述对外贸易额(X)与主要港口集装箱吞吐量(Y)之间的关系。对于一个已知的对外贸易额(X),利用得到的回归方程,去预测主要港口集装箱吞吐量(Y)的值将被认为是合理的。
的我国主要港口集装箱吞吐量与对外贸易相关性回归的估计方程。在这里港口集装箱吞吐量的估计回归方程的斜率(b1=0.543)是正的,说明随着我国对外贸易额的增长,港口集装箱吞吐量也随之增加。确切地说,如果我国对外贸易额每增加 1 亿美元,港口集装箱吞吐量将增加 5 430TEU,我们还可以说,对外贸易额每增加 1 个百分点,主要港口集装箱吞吐量将增加 0.543 个百分点,反之亦然。应用最小二乘法得到的估计的回归方程似乎可以满意地描述对外贸易额(X)与主要港口集装箱吞吐量(Y)之间的关系。对于一个已知的对外贸易额(X),利用得到的回归方程,去预测主要港口集装箱吞吐量(Y)的值将被认为是合理的。

 的回归方程去估计港口集装箱吞吐量的应变值将会产生一个误差,SSE 就是这一误差的度量。经计算,得到 SSE=464 399;离差给出了利用港口集装箱吞吐量统计样本平均值(Y)去估计港口集装箱吞吐量所产生误差的一个度量,这就是总的平方和 SST=8 664600;回归平方和测定了回归线上港口集装箱吞吐量的预测值与港口集装箱吞吐量平均值有多大的偏离问题SSR=8200200,它使我们对 Y的回归方程的可靠性有了进一步的认识。
的回归方程去估计港口集装箱吞吐量的应变值将会产生一个误差,SSE 就是这一误差的度量。经计算,得到 SSE=464 399;离差给出了利用港口集装箱吞吐量统计样本平均值(Y)去估计港口集装箱吞吐量所产生误差的一个度量,这就是总的平方和 SST=8 664600;回归平方和测定了回归线上港口集装箱吞吐量的预测值与港口集装箱吞吐量平均值有多大的偏离问题SSR=8200200,它使我们对 Y的回归方程的可靠性有了进一步的认识。


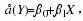 如果
如果 的值是零,则
的值是零,则
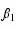 的值是否等于 0的假设检验。
的值是否等于 0的假设检验。
 的方差δ2是港口集装箱(Y)值关于回归直线的方差,我们称因变量的值对于估计的回归直线的离差为残差。在统计学上,残差和误差平方和是实际观测值关于估计的回归变异性的度量。为获得δ2的估计量,我们用误差平方和除以它的自由度,得到均方误差(MSE)。
的方差δ2是港口集装箱(Y)值关于回归直线的方差,我们称因变量的值对于估计的回归直线的离差为残差。在统计学上,残差和误差平方和是实际观测值关于估计的回归变异性的度量。为获得δ2的估计量,我们用误差平方和除以它的自由度,得到均方误差(MSE)。

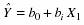 的估计量的标准误差为 182。据此,可以对估计模型进行适度的校正,标准误差182的值还是较小的,说明港口集装箱吞吐量与对外贸易额的回归模型还是有效的。
的估计量的标准误差为 182。据此,可以对估计模型进行适度的校正,标准误差182的值还是较小的,说明港口集装箱吞吐量与对外贸易额的回归模型还是有效的。
共页 总计条记录 首页 前一页 当前为第页 下一页 最后一页转到